Elementary Statistics

Statistics and Probability

Abdullah Al Mahmud

VII

Topics

• Frequency Distribution
• Histogram
• Mode

Information and Data

• Data: Raw, unstructured
• Information: Processed, organized, and structured data
• Temperature at various cities: 30, 31, 30, 29, 28, 27, 28, 29, 30, 31, 32, 33, 32, 31, 30, 29, 28, 27, 26, 26, 25, 25, 24, 24
• Lowest: 24, Highest: 33, \(\bar X = 28.7\)
• Which data and which information?

Sources of Data

• Primary: Obtained directly (not collected from someone else)
• Secondary: Using pre-collected data from someone else/some organization
• A researcher buys data from BMD to build a model of rainfall behavior
• A researcher runs an experiment to measure speed of light using a novel technique.
• A researcher makes use of the data generated by the one in example 2

Organized vs Unorganized data

• Unorganized: Messy, chaotic, raw
• Organized: Formatted, easy to understand (sorted/tabluated)

Frequency Distribution Example

Marks of students in a class

Class Interval	Frequency
41 - 50	5
51 - 60	10
61 - 70	18
71 - 80	12
81 - 90	8
91 - 100	3

• How does it help us?

Frequency Distribution

Three things required

• Range \(R=X_H-X_L+1\)
• Class Interval (CI)
• No. of class, \(k = \frac{R}{CI}\)
• CI=?

Make a frequency distribution

The number of daily customer visits to a supershop over 25 consecutive days:

32, 28, 35, 41, 29, 30, 38, 45, 27, 25

33, 40, 31, 29, 36, 42, 26, 24, 34, 39,

30, 28, 37, 33, 29

Discrete vs Continuous Intervals

• (11-15), (16-20), (21-25)
• (10-20), (20-30), (30-40)
• What is the problem with discrete intervals?
• What about interval width in each case?

Histogram

Explain the histogram

IX-X Statistics

Chapter Overview

• Data presentation
• Frequency and cumulative frequency
• Frequency distribution
• Variable types
• Frequency polygon
• Ogive

• Central Tendency
• Arithmetic Mean (AM)
• Short-cut method
• Weighetd Mean
• Median
• Mode

Why Organizing is Required

The ages of 20 participants in a fitness program were recorded and found to be as follows:

25, 30, 28, 35, 40, 38, 26, 32, 36, 31,

27, 33, 29, 41, 42, 37, 34, 39, 43, 45

What do understand by looking?

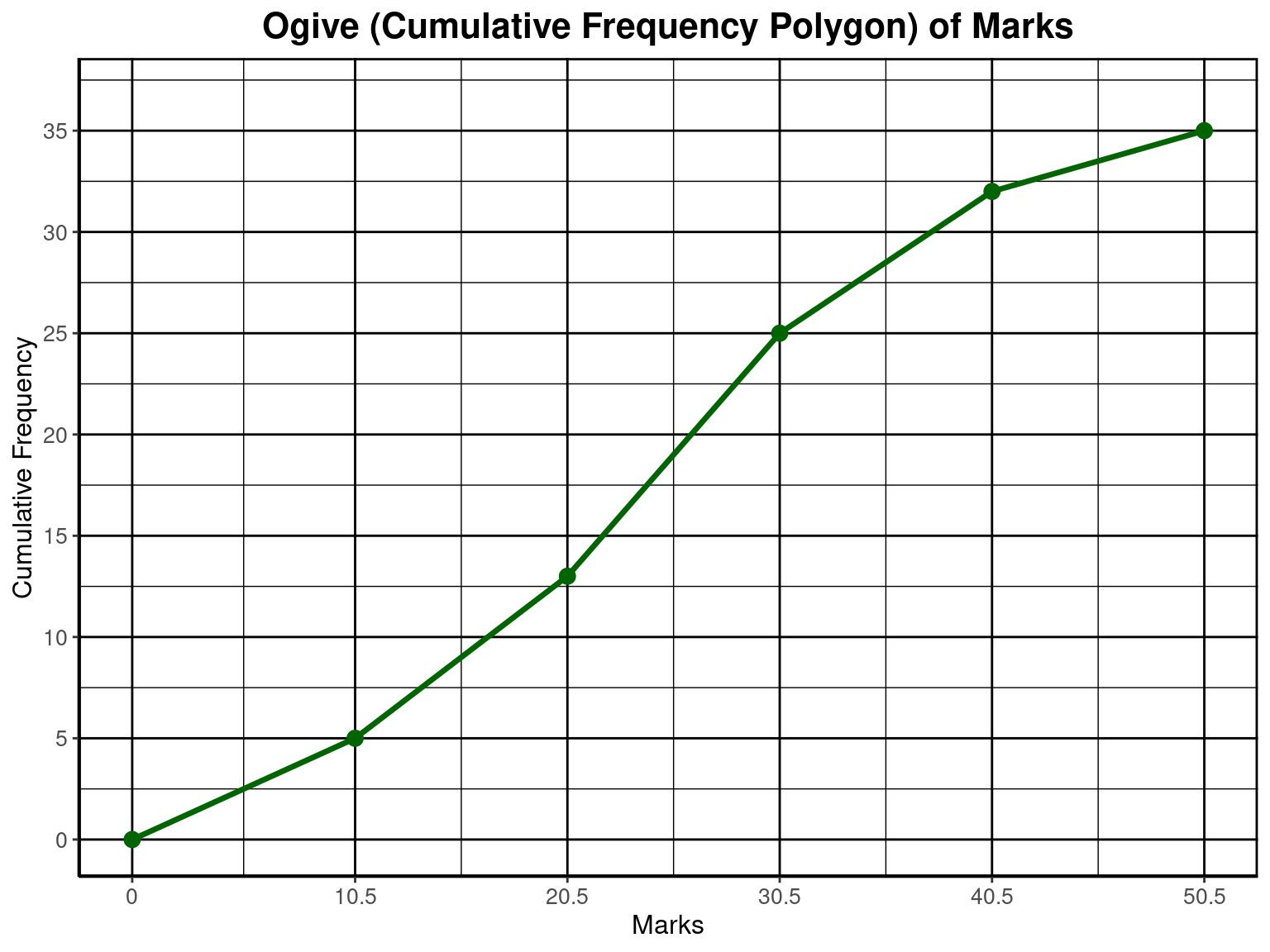
Cumulative Frequency

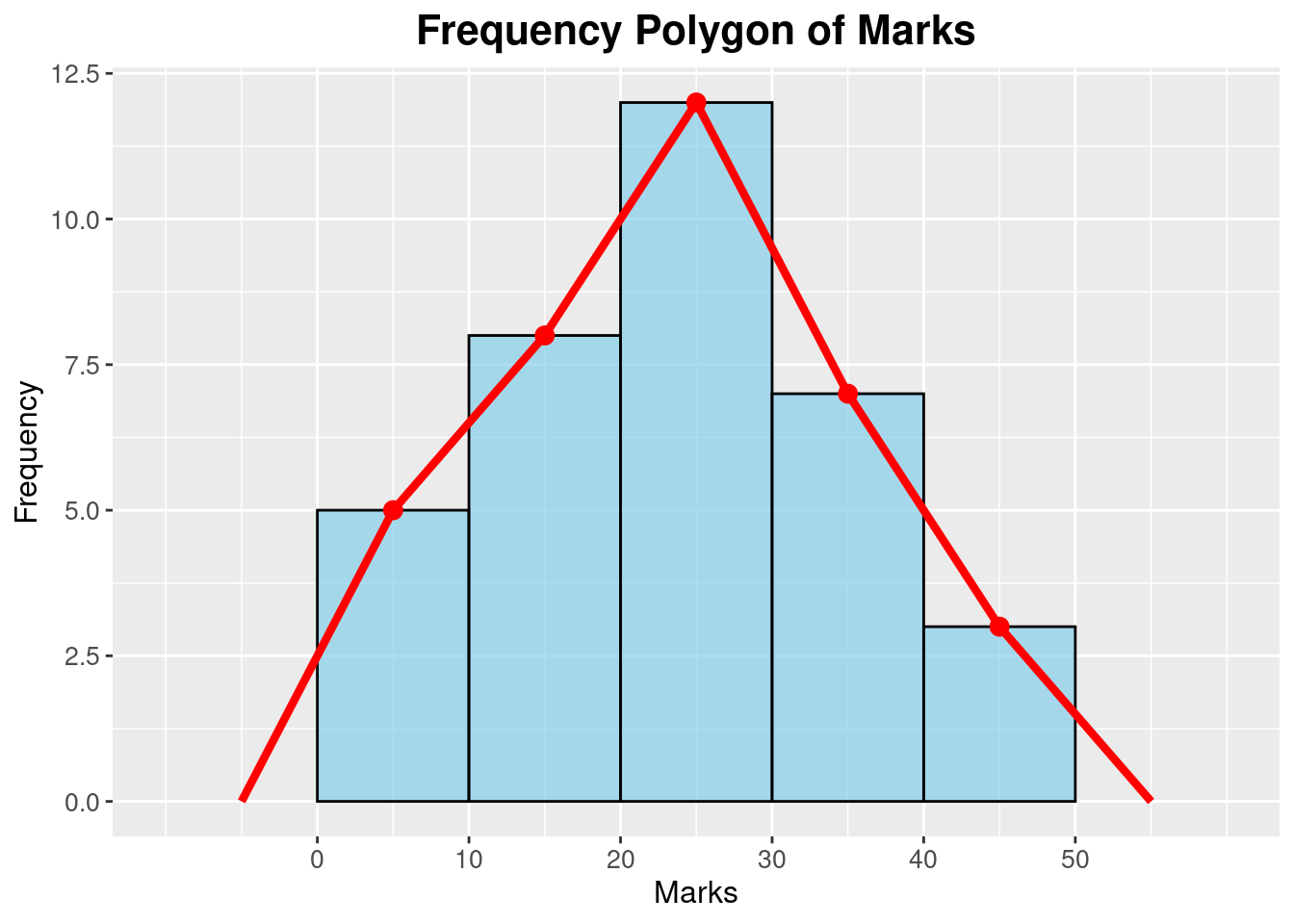
Marks	Frequency	Cumulative Frequency
0 - 10	5	5
11 - 20	8	13
21 - 30	12	25
31 - 40	7	32
41 - 50	3	35

Frequency Distribution

Three things required

• \(Range, R = X_H - X_L\)
• No. of classes (k) &
• Class Interval (CI)
• Let k or CI & find the other
• \(CI = \frac{Range}{\text{Number of classes (k)}}\)
• \(\text{Number of classes, k}= \frac{Range}{\text{CI}}\)

To Make Frequency Distribution

• Make the intervals
• Use Tally symbols to get frequencies

Variable types

Discrete

• Isolated/specific values
• Not just Integers!
• Example: number of goals, grade in a subject

Continuous

• Any value between any two value possible
• Example: Height, radius

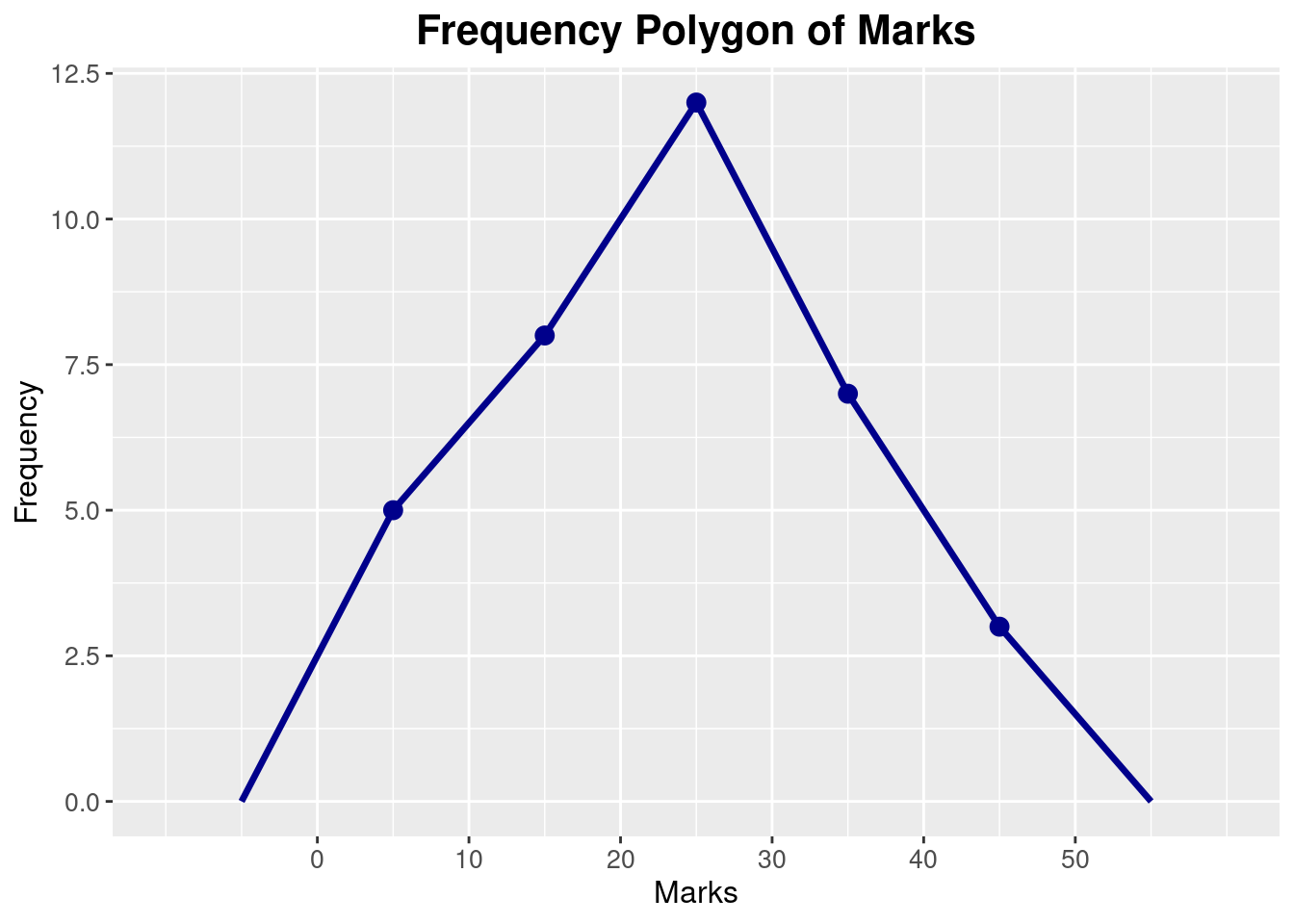
Frequency polygon

Clean Polygon

Ogive

Arithmetic Mean

• \(\bar{X} = \displaystyle \frac{\sum_{i=1}^{n} X_i}{n}\)
• Grouped/Classified data: \(\displaystyle \bar{X} = \frac{\sum_{i=1}^{k} f_i x_i}{\sum_{i=1}^{k} f_i} = \frac{\sum_{i=1}^{k} f_i x_i}{N}\)

Grouped Data

\(\displaystyle \bar{X} = \frac{\sum_{i=1}^{k} f_i x_i}{\sum_{i=1}^{k} f_i} = \frac{\sum_{i=1}^{k} f_i x_i}{N}\)

Find AM

• 2, 2, 3, 4, 5, 6, 6
• Make a table

Weighted Mean

Weighetd mean: \(\displaystyle \bar{X}_w = \frac{\sum_{i=1}^{n} w_i X_i}{\sum_{i=1}^{n} w_i}\)

• Weight: Importance of marks by judge
• Credit of subject/course

Course	Marks	Credit
Simulation	83	2
Probability	75	4
Econometrics	92	3

*Credit is weight

Find \(\bar X\)

Interval	Frequency
1 - 10	7
11 - 20	14
21 - 30	21
31 - 40	17
41 - 50	9
51 - 60	4

• USe mid-values as \(x_i\)

AM Short-cut Method

Concept

Find \(\bar x\)

1000, 1010, 1020, 1030, 1040

Be Smart!

• Subtract 1000 \(\rightarrow\)
• \(\bar X = a + \frac{\sum f_i u_i}{n} \times h\)
• Find it from previous table
• Does the value of a matter?

Shor-cut AM Example

Interval	mid-value (\(x_i\))	frequency (\(f_i\))	\(u_i = \frac{x_i-a}{h}\)	\(f_iu_i\)
1 - 10	5.5	7
11 - 20	15.5	14
21 - 30	25.5	21
31 - 40	35.5	17
41 - 50	45.5	9
51 - 60	55.5	4

Median

What is the median?

2, 3, 5, 8, 10

• Explain median
• What now: 5, 4, 3, 9
• \(\frac{n+1}{2}\) for odd n
• \(\frac{nth + (n+1)th}{2}\) for even n

IX-X Probability