Introduction to Statistics

Abdullah Al Mahmud

Statistics: What & How

Topics

• What is statistics?
• How Statistics works?
• Probability and Statistics
• Application of Statistics
• Example Problem

What is statistics?

Three Meanings

• Plural of statistic
• Table of data
• Methodology

How Statistics works?

Takes a sample from a population.

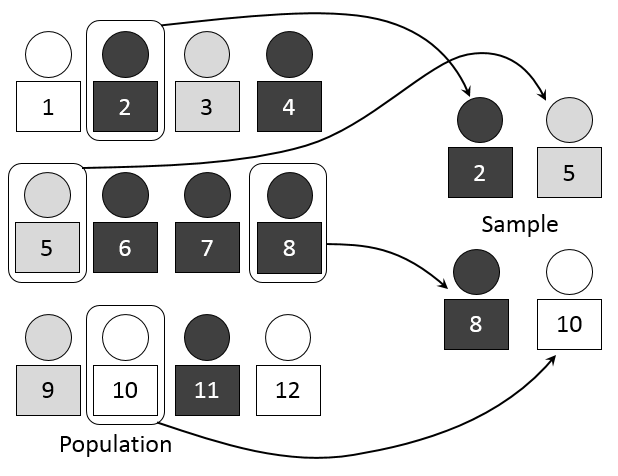
There are many sampling techniques.

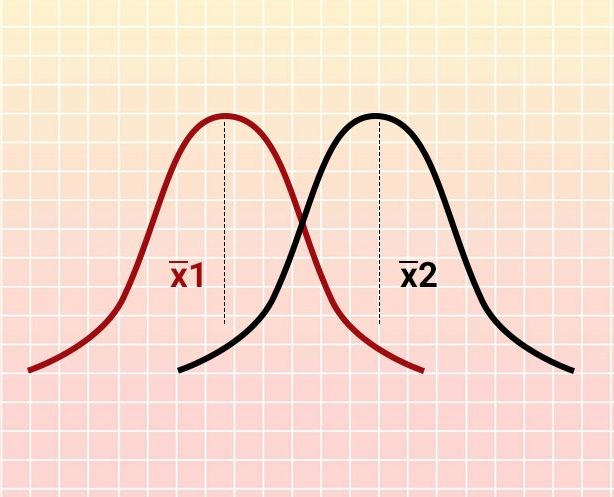
Probability and Statistics

Application of Statistics

Examples

• Identification of unwanted spam messages in e-mail
• Segmentation of customer behavior for targeted advertising
• Forecasts of weather behavior and long-term climate changes
• Prediction of popular election outcomes
• Development of algorithms for auto-piloting drones and self-driving cars
• Optimization of energy use in homes and office buildings
• Projection of areas where criminal activity is most likely
• Discovery of genetic sequences linked to diseases

End of This Segment

THANK YOU!

Chapter 01: Basic Concepts

Chapter Overview

• Definition
• Population and sample
• Variable and its types
• Scale of measurement
• Use of summation sign
• Summation theorems
• Mathematical Problems

Definition

Coxton and Crowden

Statistics may be defined as the science of collection, presentation, analysis and interpretation of numerical data.

Mechanism

• Data Collection
• Organization
• Analysis
• Interpretation
• Presentation

Population and Sample

Population: A set of similar items or events which is of interest Sample: Any subset of population

Population Types

• Finite
• Infinite

Examples

Group/collection of –

• students in a classroom
• stars in the sky
• possible outcomes when flipping a coin repeatedly
• books in a library
• water molecules in the ocean
• employees in a company

Variable and Constant

• Variable
• Random Variable
• Constant

• \(\pi\)
• Name of students
• Result of a die throw

Variable Examples

• Income of a regular employee
• Income of a freelancer
• Any unchanging number, e.g, \(\pi\)
  
• Result of a die throw
• Father’s name
• Mark of a subject
• GPA of a student

Types of Variable

• Qualitative \(\rightarrow\) numeric
• Quantitative \(\rightarrow\) non-numeric
• Discrete: Limited and pre-specified
• Continuous: Can take on any values between any two given number

Univariate, Multivariate

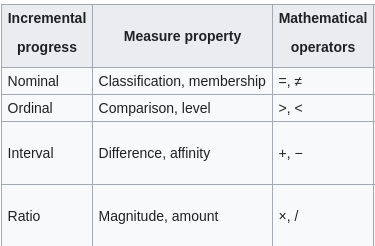
Scale of Measurement

Describes nature of information within the values.

• Nominal: Name of Insignificant number, e.g., color, Street no.,
• Ordinal: Order matters, e.g., rating
• Interval: Zero may not be zero, like temperature, IQ
• Ratio: Zero is 0; most variables fall in this category

Examples

• Gender
• Religion
• Temperature
• Income group (Lower class, Low, Middle, High)
• Income
• Distance of stars
• Radius of screws
• Diameter of trees
• Room no.

Another Example

Match as per suitable scale

Movie Rating	Scale
Poor, bad, good, excellent	ratio
In a scale of -10 to 10: -10, -2, 0, 5, 10	interval
Awesome, Amazing, Mind-blowing, Stunning	nominal
In a scale of 0 to 10: 0, 5, 8, 10	ordinal

Examples of Interval Scale

Multiplication/division cannot be carried out

• Temperature (Celsius scale)
• Dates (AD)
• Location in Cartesian coordinates
• Direction measured in degrees

For more see here and Interval Scale discussion on Stat Mania

Operation with scales

Shifting origin and scale

Say we have values, \(x_1, x_2, \cdot \cdot \cdot , x_n\)

• Origin shift: Adding/Subtracting
• \(y_1 = x_1-a \space or \space x_1+a\)
• Scale shift: Multiplying/Division
• \(y_1 = b \cdot x_1 \space or \space x_1/b\)
• both: \(y_i = \frac{x_i-a}{b}\)
• Why might we need it?

Use of Summation sign

• \[x_1 + x_2 + x_3 + x_4 = \sum_{i=1}^4 x_i\]
• \[x_1 + x_2 + ... x_n = \sum_{i=1}^n x_i\]
• \[x_1 + x_2 + ... x_{10} = ?\]

Theorem 01: \(\Sigma bx_i\)

\[\sum_{i=1}^n bx_i=b \sum_{i=1}^n x_i\]

Theorem 02: \(\Sigma (ax_i-b)\)

\[\sum_{i=1}^n (ax_i-b)=a \sum_{i=1}^n x_i-nb\]

Quick tips

• \(\sum_{i=1}^n a = na\)
• Can you prove it?

Theorem 03: \(\Sigma (ax_i^2-bx_i+c\)

\[\sum_{i=1}^n (ax_i^2-bx_i+c)=a\sum_{i=1}^n x_i^2-b\sum_{i=1}^n x_i + nc\]

Theorem 04: \(\Sigma (ax_i-by_i)\)

\[\sum_{i=1}^n (ax_i-by_i)=a\sum_{i=1}^n x_i - b \sum_{i=1}^n y_i\]

Theorem 05: \(\Sigma (ax_i-b)^2\)

\[\sum_{i=1}^n (ax_i-b)^2=a^2 \sum_{i=1}^n x_i^2 - 2ab \sum_{i=1}^n x_i + nb^2\]

Theorem 06: \((\sum_{i=1}^n x_i)^2\)

\[(\sum_{i=1}^n x_i)^2=\sum_{i=1}^n x_i^2 + \sum_{i \ne j}^n\sum x_ix_j\]

Quick Tip

\[\prod_{i=1}^k x_i = x_1 \times x_2 \times \cdot \cdot \cdot \times x_n\]

Theorem 07: \(\prod_{i=1}^k x_iy_i\)

\[\prod_{i=1}^k x_iy_i = (\prod_{i=1}^k x_i)(\prod_{i=1}^k y_i)\]

Double Summation Example

X	20	25	15
Y	15	30	20

• \(20 \times 15 + 20 \times 30 + 20 \times 20 \rightarrow x_1 \times y_j\)
• \(25 \times 15 + 25 \times 30 + 25 \times 20 \rightarrow x_2 \times y_j\)
• \(15 \times 15 + 15 \times 30 + 15 \times 20 \rightarrow x_3 \times y_j\)
• Row to row \(rightarrow x\) varies but \(y_j\) is constant

Theorem 08: \(\Sigma \Sigma (x_i+y_j)\)

\(\displaystyle \sum_{i=1}^m \sum_{j=1}^n (x_i+y_j)=n\sum_{i=1}^m x_i + m \sum_{i=1}^n y_j\)

• \(\displaystyle \sum_{i=1}^m (x_i+y_1+x_i+y_2+\cdots+x_i+y_n)\)
• \(\displaystyle \sum_{i=1}^m \{(x_i+x_i+\cdots \text{up to n})+(y_1+y_2+\cdots+y_n)\)
• \(\displaystyle \sum_{i=1}^m(nx_i+\sum_{j=1}^ny_j)\)
• \(\displaystyle (nx_1+\sum_{j=1}^ny_j+nx_2+ \sum_{j=1}^ny_j)+\cdots+nx_m+\sum_{j=1}^ny_j))\)
• \(\displaystyle n\sum_{i=1}^m x_i+m\sum_{j=1}^ny_j\)

Theorem: \(\Sigma \Sigma x_iy_j\)

\(\displaystyle \sum_{i=1}^m \sum_{i=1}^n x_iy_j=(\sum_{i=1}^n x_i) (\sum_{i=1}^n y_j)\)

• \(\displaystyle \sum_{i=1}^m (x_iy_1+x_iy_2+\cdots+x_iy_n)\)
• \(\displaystyle \sum_{i=1}^m x_i(y_1+y_2+\cdots+y_n)\)
• \(\displaystyle \sum_{i=1}^m x_i \sum_{i=1}^n y_i\)

Problem -01

Given

\(f_1=2, f_2 = 4, f_3 = 6\)

\(x_1 = -3, x_2 =7, x_3 = 4\)

Find the values of

1. \(\sum f_ix_i\)
2. \(\sum f_ix_i^2\)
3. \(\sum f_i(x_i-5)^2\)

Problem - 02

13. Find the value of \(\sum_{i=1}^{10} (x_i-4)\)

where \(\sum_{i=1}^{10} x_i = 20\)

Problem - 03

• Discrete vs continuous variable
• Prove \[\sum_{i=1}^k abx_i = ab \sum_{i=1}^k x_i\]

Problem - 04

Prove \[\prod_{i=1}^n c =c^n\]

Problem - 05

13. Find the value of

\[\sum_{i=1}^{10} (x_i-4)\] where \[\sum_{i=1}^{10}=20\]

Problem - 06

\(\displaystyle \sum_{i=1}^{10} x_i = 20, \sum_{i=1}^{10} x_i^2 = 400\)

Find the value of \(\displaystyle \sum_{i=1}^{10} (x_i^2+5x_i+10)\)

Problem - 07

X	20	25
Y	15	30

1. Prove Sum of Square \(\ne\) Square of Sum
2. Prove \(\displaystyle \sum X_iY_i \ne \sum \sum X_iY_i\)

Creative Questions

Look here

Creative Question - 02

Income (x)	120	130	88	150	175	144	180	200	160	155
Expense (y)	80	120	70	100	160	114	170	195	140	131

Prove

• \(\displaystyle \sum_{i=1}^{10} \sum_{j=1}^{10}x_iy_j=(\sum_{i=1}^{10}x_i)(\sum_{j=1}^{10}y_j)\)$
• \(\displaystyle \sum_{i=1}^{10} \sum_{j=1}^{10}(x_i-y_j)=10 \times \sum_{i=1}^{10}x_i- 10 \times \sum_{j=1}^{10}y_j\)
• \(\displaystyle \sum_{i=1}^{10}x_iy_i \ne (\sum_{i=1}^{10}x_i)(\sum_{i=1}^{10}y_j)\)

End of Chapter 01!